Why Floyd–Warshall algorithm works

Question Thrown

All we know that Floyd–Warshall algorithm is a dynamic programming algorithm aims to solve the all-pairs shortest path problem. the code itself is simple as follows:

for (int k = 0; k < n; k++) {
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      if (dist[i][k] + dist[k][j] < dist[i][j]) {
        dist[i][j] = dist[i][k] + dist[k][j];
      }
    }
  }
}

Shown already in the most common blogs that k standards for the intermediate node. dist[i][j] = dist[i][k] + dist[k][j]; updates the shortest path from i to j through k. Now a natural question is why this works since dist[i][k] and dist[k][j] are not necessarily the shortest path from i to k and k to j respectively.

Takeaway

The above thought k stands for the intermediate node is nearly correct. It actually stands for all [0, k] can be taked as the intermediate nodes to get the dist[i][j]. so when we traverse to the final k, aka k = n - 1, dist[i][j] would be updated with the meaning: the shortest path from i to j through all nodes [0, n - 1].****

Analysis

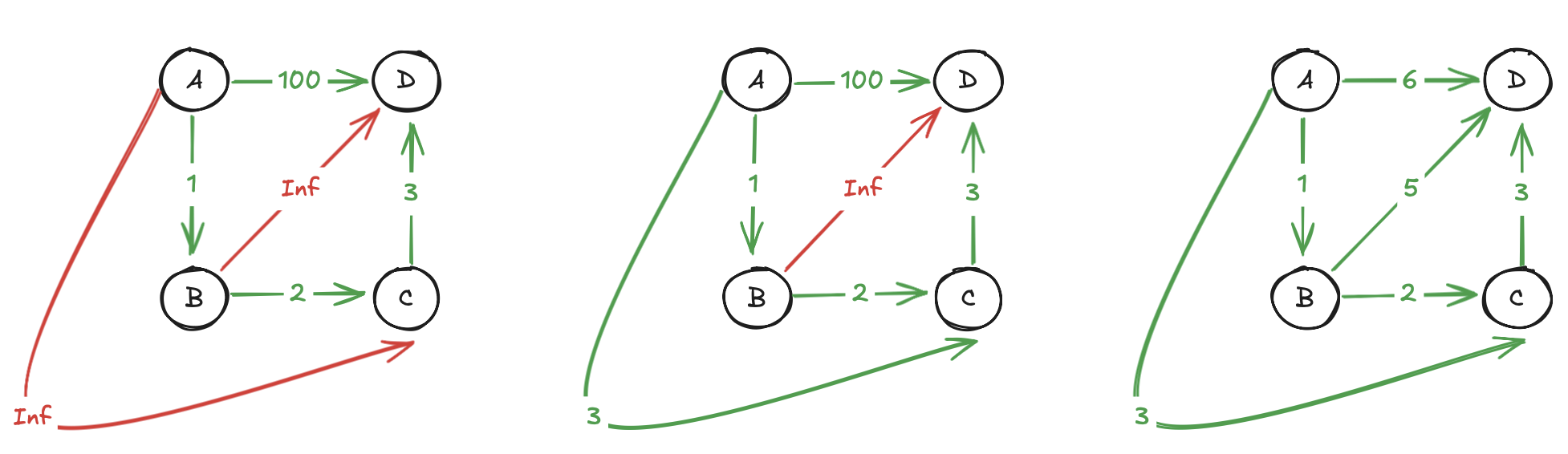
• Initial step: the left pic
• while k == 0: updates all pairs through A. since the in-degree of A equals to 0, so we do not show the pic.
• while k == 1: Since we’ve already passed step2, so implicitly this steps actually updates all pairs through B (and A). Shown in pic2.
• while k == 2: Similarly to step3, Updating all pairs through C (and A, B)

  More about final step. Take A->D as example. The corrosponding updating code: dist[A][D] = dist[A][C] + dist[C][D];. Answering to the first question in the first of the article. dist[A][C] has already been updated by dist[A][B] + dist[B][C] which means dist[A][C] in this time have already considered the info of A, B, C.